X. Zasada względności w czasoprzestrzeni
Do analizy warto zawsze wybrać na początku najprostszy model. Dlatego nasze rozważania rozpoczniemy od jednowymiarowej przestrzeni, którą możemy sobie wyobrażać, jako prostą p, w której mamy nieruchomego obserwatora O. Jeżeli dodamy czas, jako prostą t ortogonalną do przestrzeni p, to otrzymamy dwuwymiarową czasoprzestrzeń (rys. 8).
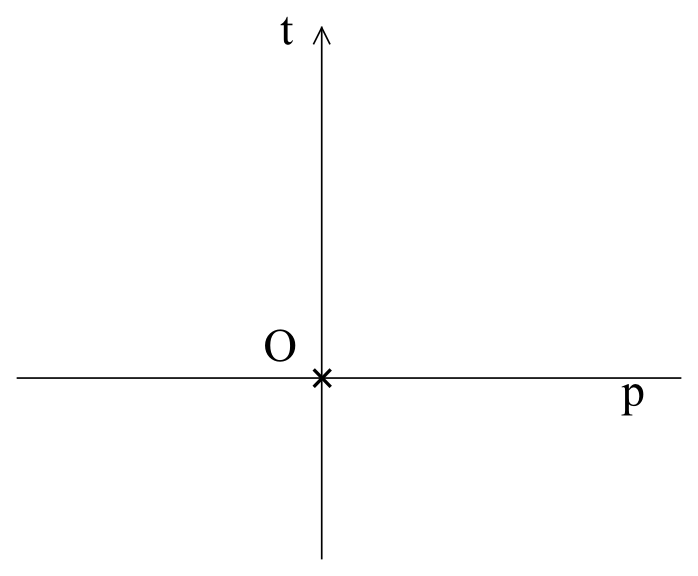
Rysunek 8
Zakładamy, że nasz obserwator nie rusza się w przestrzeni (czy dokładniej: nie rusza się względem systemu współrzędnych, który jest z nim powiązany), to znaczy, że w czasoprzestrzeni będzie poruszać się tylko w kierunku osi t i w kolejnych chwilach t1, t2, t3 będzie znajdował się w punktach t1, t2, t3 na osi t (rysunek 9).
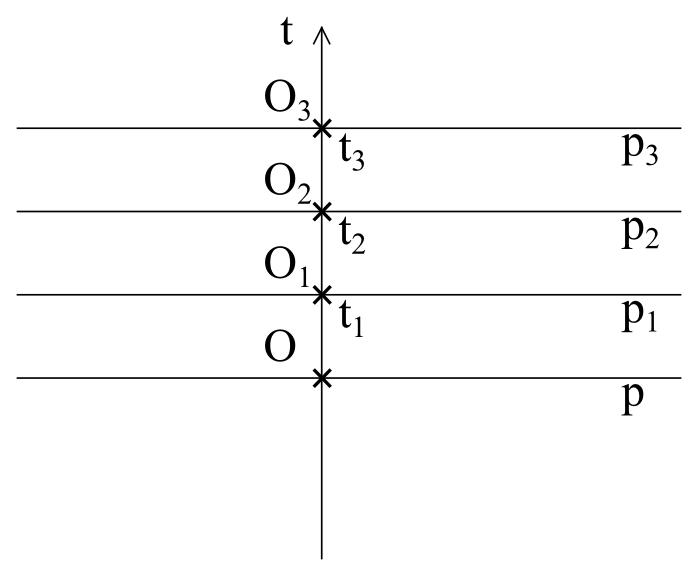
Rysunek 9
Dodajmy do naszego modelu jeszcze jedneg1o obserwatora P, który będzie się od obserwatora O oddalać ruchem prostoliniowym jednostajnym. Jego tor w czasoprzestrzeni będzie tworzył prostą nachyloną względem osi czasu obserwatora O pod pewnym kątem, zależnym od szybkości, jaką się obserwator P oddała od obserwatora O (rysunek 10).
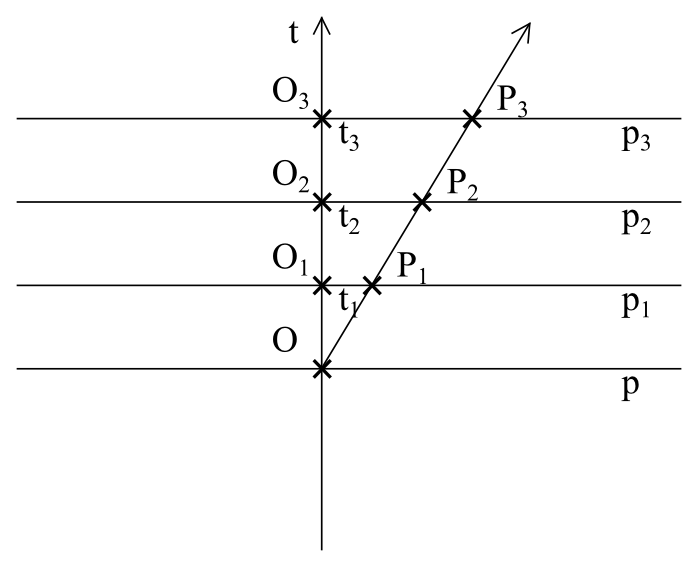
Rysunek 10
Zasada względności mówi nam jednak, że ruch jest względny. Jeżeli mamy dwóch obserwatorów, którzy od siebie się oddalają, nie da się stwierdzić, który jest w spoczynku a który w ruchu. To znaczy, że obserwator P może twierdzić, że to on nie rusza się w przestrzeni a obserwator O oddała się od niego. Dla niego czas płynie w kierunku jego ruchu w czasoprzestrzeni, czyli wzdłuż linii u a przestrzeń przebiega dla niego w kierunku linii r (rysunek 11).
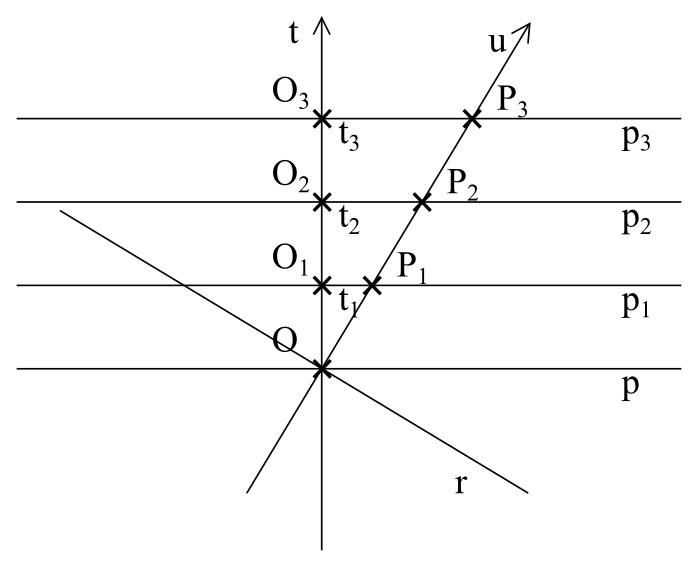
Rysunek 11
Jeżeli trzymamy się zasady względności, to sytuacja obserwatora O i obserwatora P musi być analogiczna.
Ze względu na to, że całą operację możemy powtarzać rozpoczynając od obserwatora P i prędkość oddalania się następnego obserwatora możemy zmieniać, wydaję się, że w naszej czasoprzestrzeni może przestrzeń i czas przebiegać w dowolnym kierunku. Ponieważ światło dla każdego obserwatora musi poruszać się tak samo, oznacza to, że rozprzestrzenia się z tą samą szybkością we wszystkich kierunkach czasoprzestrzeni i że dla światła nie istnieje czas.
Od razu jednak widać kilka problemów. Na przykład co to właściwie jest szybkość światłą, jeżeli dla światła nie płynie czas i cała czasoprzestrzeń dla niego oznacza tylko przestrzeń. Albo jeszcze poważniejszy problem dotyczący przyczynowości. Jeżeli kierunek czasu w czasoprzestrzeni może być dowolny, to dla dwóch różnych obserwatorów może biec w przeciwnym kierunku. To naruszałoby przyczynowość. W tym miejscu musimy w naszych rozważaniach zatrzymać się i pomyśleć, gdzie jest błąd i które nasze założenia trzeba zmienić.
Znalezienie rozwiązania często bywa trudne właśnie dlatego, że niektóre założenia przyjmujemy nie świadomie. Jesteśmy nauczeni i przyzwyczajeni do pewnych poglądów i wcale o nich nie myślimy jako o założeniach. Także nie jest łatwo wpaść na to, że problem z przyczynowością może być spowodowany tym, że piszemy i rysujemy na płaskiej kartce papieru i że w wyniku tego nasz model jest plaski. Tylko jeżeli nie płaski, to jaki? Pierwszym pomysłem jest, że płaszczyznę zaczniemy zginać i zrobimy z niej powierzchnię kuli. Tylko że kula nie tylko nie rozwiązuje problemu, ale jeszcze stwarza następny: co się stanie, jeżeli obserwator obiegnie w czasie całą kulę i powróci do miejsca, w którym był na początku? Wszystkie tę problemy jednak znikną, jeżeli kula zacznie się rozszerzać. Otrzymamy inne wyobrażenie o czasie. Czas tu ma dwa wymiary. Czas lokalny, różny dla różnych obserwatorów, który w zależności od szybkości ma różny kierunek w czasoprzestrzeni i czas kosmiczny w kierunku rozszerzania się czasoprzestrzeni, który w danym punkcie jest jednakowy dla wszystkich obserwatorów i dotyczy także światła. W takim modelu nie jest naruszona zasada przyczynowości, bo chociaż czas lokalny dwóch obserwatorów płynie w odwrotnym kierunku, to czas kosmiczny powoduje, że kolejność zdarzeń jest zachowana.

